donde
es la media general, 
el efecto de la i-ésima fila, 
el efecto de la j-ésima columna, 
el efecto del k-ésimo tratamiento y 
el error aleatorio.
Enfoque Clásico
En este tipo de pruebas se utiliza el análisis de varianza para
detectar las fuentes de variación, aquí se expresan las observaciones
en un cuadrado latino como:
donde
es la media general,
el efecto de la i-ésima fila,
el efecto de la j-ésima columna,
el efecto del k-ésimo tratamiento y
el error aleatorio.
as hipótesis de interés en el diseño clásico son:
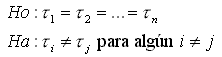
En estudios de mejoramiento de plantas, por ejemplo, las diferencias entre tratamientos son relativamente pequeñas. Esas pequeñas diferencias no son detectadas eficientemente por la prueba clásica. Hay pruebas mas eficientes que la prueba F clásica como por ejemplo las pruebas basadas en rangos o en rachas que se presentan a continuación.
Rangos
El rango de una observación es el lugar que ocupa al ordenar
todas las observaciones de una muestra (o de cualquier grupo de observaciones)
en orden ascendente. Las pruebas estadísticas basadas en rangos
comparan los cuadrados de las diferencias entre las sumas de rangos por
tratamiento y los valores esperados de la suma de rangos. En las pruebas
por rangos se definen las observaciones como:
y las hipótesis de interés son:
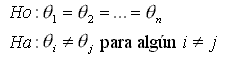
El rango de una observación se define como:
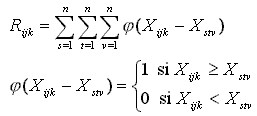
Rachas
Las rachas (o secuencias) son sucesiones de uno o más símbolos
idénticos que pueden ser precedidos ó seguidos por un símbolo
diferente o por ningún símbolo. En el diseño en cuadrado
latino las observaciones deben transformarse en número de rachas
para realizar las pruebas correspondientes.
El procedimiento usual consiste en ordenar las observaciones y policotomizar la muestra utilizando los números de tratamientos para formar una sucesión:
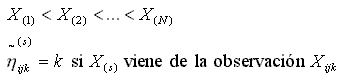
El número de rachas para cada observación es el número
de la racha en la que se encuentra dicha observación y se denota
con el símbolo 
.
Las pruebas basadas en rachas utilizan también los números
medios de rachas totales y por tratamiento, y sus diferencias cuadráticas
para detectar los efectos de los tratamientos (es decir, las diferencias
entre sus parámetros de localización).
El cálculo formal de
se lleva a cabo utilizando variables indicadoras que permiten contar el
número de veces que la sucesión cambia de símbolo
asi:
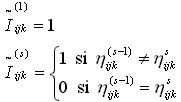
Con las variables aleatorias 
se construye la sucesión:
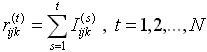
que indica el número de rachas hasta la t-ésima estadística
de orden o hasta la observación 
.