)
de las distribuciones de probabilidad de los tratamientos muestreados son
iguales.
El diseño en cuadrado latino
Este diseño es técnicamente un modelo restringido de
tres vías, como diseño experimental permite convertir en
factibles proyectos estadísticos en los que el costo de la toma
de muestras es un factor relevante, pues reduce la necesidad de tomar muchas
muestras con el fin de encontrar diferencias entre tratamientos aplicados.
Este diseño se utilizó por primera vez en la década
de los 60's en investigaciones agrícolas.
El modelo en cuadrado latino permite establecer diferencias entre n
tratamientos organizados en una matriz de n x n cuyas filas
y columnas se encuentran pseudoaleatorizadas, esto es, se encuentran
organizadas de tal forma que en cada fila y columna aparece una y solo
una muestra de cada tratamiento, así, es necesario tomar sólamente
n^2 (n de cada tratamiento) muestras en vez de n^3 muestras necesarias
para realizar estudios organizados con otro tipo de diseños.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
El cuadrado latino que se muestra en la figura es uno de los tantos
posibles para el tamaño 4x4, este se considera un modelo aleatorizado
pues cualquier intercambio entre filas o columnas genera un cuadrado pseudoaleatorio
como el de la figura. Los números que aparecen en las celdas corresponden
a los números que identifican los tratamientos a analizar. Al disponer
los resultados de las muestras en este orden (o cualquier otro que cumpla
los requisitos) es posible realizar varias pruebas estadísticas
para determinar si los parámetros de localización ()
de las distribuciones de probabilidad de los tratamientos muestreados son
iguales.
En general la hipótesis que se maneja en los análisis
estadísticos para cuadrados latinos es:
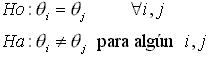
La aceptación o rechazo de ésta hipótesis permite
tomar decisiones acerca de la efectividad real de los tratamientos aplicados
al experimento. Es preciso aclarar que, entre mas grande el orden del cuadrado,
son mas confiables las estadísticas de prueba.