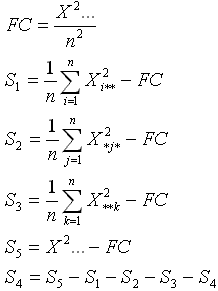
Prueba Clásica
La prueba clásica, o prueba F usa las sumas de cuadrados de
los errores de las varianzas para las filas, columnas y tratamientos para
tomar una decisión acerca de las fuentes relevantes de decisión,
esta prueba tiene distribución
F con n-1,(n-1)(n-2) grados de libertad. El procedimiento
es el siguiente:
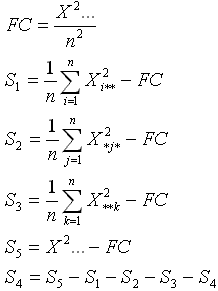
Los resultados se presentan de la siguiente manera:
|
|
|
|
|
|
| Filas |
|
|
V1 =S1 /(n-1) |
|
| Columnas |
|
|
V2 =S2 /(n-1) |
|
| Tratamientos |
|
|
V3 =S3 /(n-1) |
|
| Error experimental |
|
|
V4 = S4/ [(n-1)(n-2)] | |
| Total |
|
|
Prueba de Bennett (Rangos)
La prueba de Bennett puede expresarse como la suma de cuadrados de
las diferencias entre la suma de rangos observada y la suma de rangos esperada,
modificada por algunas constantes. Aquí se utiliza la suma de rangos
por tratamientos (ver Aspectos Generales)
y la prueba se implementa así:
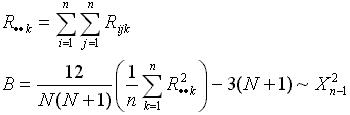
Esta prueba tiene distribución asintótica a la Chi-cuadrado con n-1 grados de libertad, y rechaza la hipótesis para valores grandes de B.
Prueba de Zimmerman (Rangos)
Zimmerman encontró que la estadística B propuesta por
Bennett, es la prueba de Kruskal-Wallis aplicada al caso particular del
diseño en cuadrado latino y propuso el siguiente test, con los mismos
supuestos para el test de Bennett se determinan los rangos por filas Rf
y por columnas Rc, con estas dos variables aleatorias se define
Zijk=Rfijk+Rcijk
Con esta nueva variable aleatoria Z, se halla la suma de los cuadrados
totales y la suma de los cuadrados de los tratamientos como en todos los
cuadrados latinos; la estadísitica de prueba propuesta es entonces:
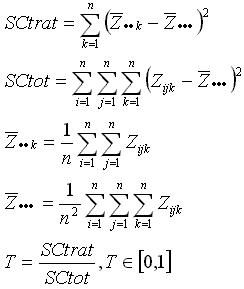
Si la hipótesis es falsa, las diferencias entre los tratamientos
y la media general son grandes, entonces
SCtrat 
SCtot
y T1, haciendo
un análisis semejante resultará que si la hipótesis
es verdadera T0.
Sin embargo, no se puede hallar la distribución exacta de T, por esto se utiliza el estadístico:
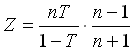
que tiene distribución asintótica a la distribución
F( n-1 , n(n-1) ) como lo demostró Zimmerman
aplicando el teorema de Wald y Walfowitz.
Prueba C (prueba de rachas basada en la suma
de cuadrados de diferencias)
En esta prueba se tienen en cuenta los números de rachas (ver
Aspectos
Generales) medios y totales por tratamiento así:
Sean:
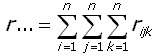
la suma total del número de rachas,
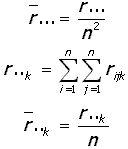
el promedio general de rachas, la suma de rachas del k-ésimo tratamiento y el promedio del número de rachas del k-ésimo tratamiento. Puesto que la prueba es para comparar tratamientos en términos de localización, la estadística de prueba está basada en las diferencias entre a media de los tratamientos y le media general de las rachas, esta estadística propuesta es:
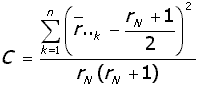
Esta estadística rechaza la hipótesis de la igualdad de
los parámetros de localización para valores grandes de C.
Para valores pequeños de n (hasta 3) se calcula la distribución
exacta de C, para valores mayores, se estima la media y la varianza de
C a partir de una muestra lo suficientemente grande y se aproxima la distribución
de C a una normal.
Para hallar la distribución exacta de C, se calculan todos los posibles arreglos distinguibles y para cada uno se halla el valor C. El número de arreglos posibles está dado por:
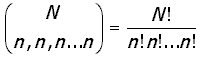
Prueba M (Prueba de rachas basada en el cociente
de sumas de cuadrados)
Esta es una prueba alternativa que evita la necesidad de calcular la
media y la varianza para aproximar la distribución, por medio de
el cociente de sumas de cuadrados, esta prueba tiene distribución
asintótica a la F (ésta hipótesis parece resultar
falsa al realizar la simulación)
La estadística de prueba propuesta es la siguiente:
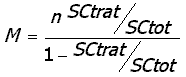
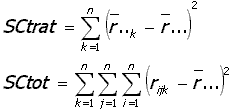
Esta estadística también rechaza la hipótesis para valores grandes de M, la distribución dice ser F con n-1, n(n-1). En la simulación se halló la distribución exacta de M para cuadrados hasta 3x3, al utilizar el supuesto de la distribución F obtenemos un total fracaso al detectar diferencias entre parámetros de localización.